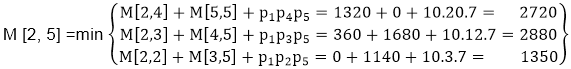The idea is to break the problem into a set of related subproblems that group the given matrix to yield the lowest total cost. Clearly, the first method is more efficient. However, the product rule of this sort does apply to the differential form (see below), and this is the way to derive many of the identities below involving the trace function, combined with the fact that the trace function allows transposing and cyclic. For example, if A is a 10 × 30 matrix, B is a 30 × 5 matrix, and C is a 5 × 60 matrix, then computing (AB)C needs (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 operations while computing A(BC) needs (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 operations. Note that exact equivalents of the scalar product rule and chain rule do not exist when applied to matrix-valued functions of matrices. However, the order in which the product is parenthesized affects the number of simple arithmetic operations needed to compute the product. For example, for four matrices A, B, C, and D, we would have: The matrix multiplication is associative as no matter how the product is parenthesized, the result obtained will remain the same. The problem is not actually to perform the multiplications but merely to decide the sequence of the matrix multiplications involved. Matrix chain multiplication (or Matrix Chain Ordering Problem, MCOP) is an optimization problem that to find the most efficient way to multiply a given sequence of matrices.
Matrix chain multiplication problem: Determine the optimal parenthesization of a product of n matrices.